p130

One-way Anova

> modelA<-aov(drugA_dose1~fatigue)

> summary(modelA)

            Df Sum Sq Mean Sq F value  Pr(>F)   
fatigue      2  1.526  0.7631   10.56 0.00105 **
Residuals   17  1.228  0.0723                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> 
> par(mfrow=c(2,2))
> plot(modelA)

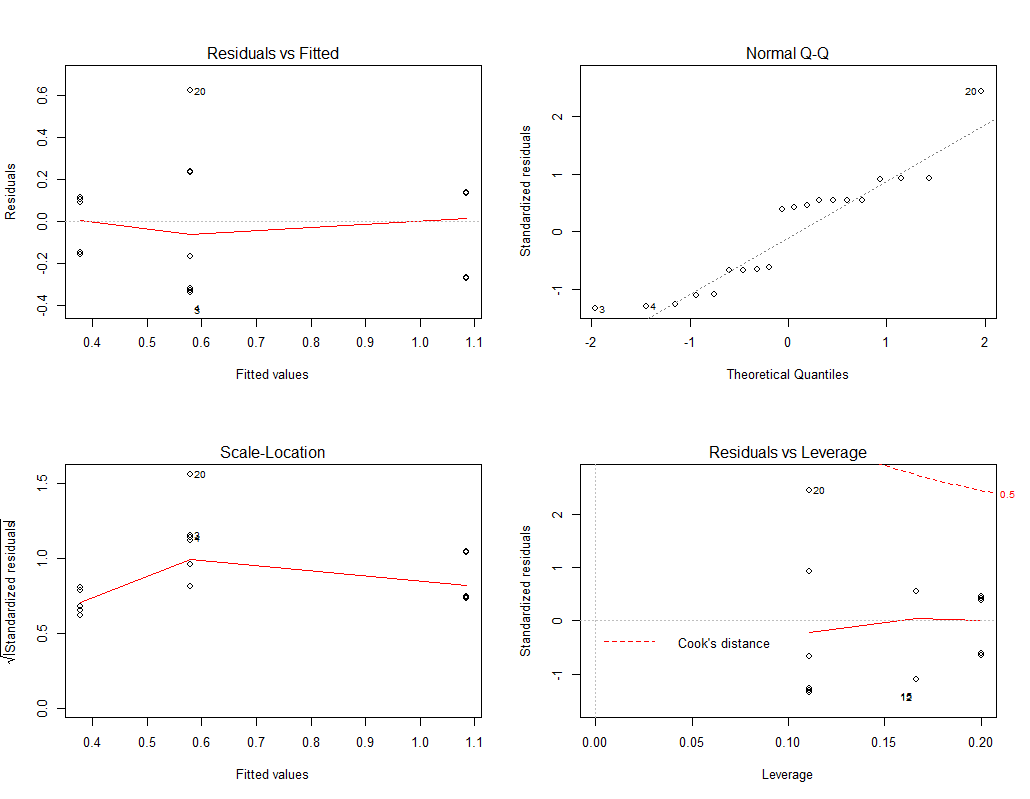
Residuals vs Filters

• 0 선을 기준으로 고르게 위아래로 분산되어 있는게 좋은 데이터이다

Normal Q-Q

• 튀는 값을 빼는 게 더 좋은 그래프가 나온다

> modelB<-update(modelA, subset = (patients !=20))

lm(y~x) - > y=a +bx

aov(y~x) -y = a + bx1 + cx2

아노바는, x는 카테고리형 변수라 그룹을 나누고, 따로 계산한다.

> summary.lm(modelB)

Call:
aov(formula = drugA_dose1 ~ fatigue, subset = (patients != 20))

Residuals:
    Min      1Q  Median      3Q     Max 
-0.2708 -0.1998  0.0920  0.1347  0.3135 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.08383    0.09099  11.912 2.29e-09 ***  # p-value가 0.05보다 작으므로 피로도는 영향이 있다

fatiguelow  -0.70583    0.13496  -5.230 8.25e-05 ***
fatiguemed  -0.58233    0.12037  -4.838 0.000182 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2229 on 16 degrees of freedom
Multiple R-squared:  0.6783,    Adjusted R-squared:  0.638 
F-statistic: 16.86 on 2 and 16 DF,  p-value: 0.0001148

T-way ANOVA

피로도 데이터에 성별을 추가하자

성별은 Factor변수 2가지 레벨, 피로도도 Factor 변수 3가지 레벨(Low, Med, High) 이다

> patient.sex <- as.factor(c("F", "F", "F", "M", "M", "F", "M", "M", "M", "F", "F", "M", "M", "F", "F", "F", "M", "M", "F", "M"))

> modelC = aov(drugA_dose1 ~ fatigue*patient.sex) #데이터는 

> summary(modelC)
                    Df Sum Sq Mean Sq F value Pr(>F)   
fatigue              2 1.5261  0.7631   8.980 0.0031 **   # p-value가 0.05보다 작으므로 피로도는 영향이 있다
patient.sex          1 0.0128  0.0128   0.151 0.7038      # 환자와 성별은 의미가 없다
fatigue:patient.sex  2 0.0260  0.0130   0.153 0.8594      # 
Residuals           14 1.1896  0.0850                  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

굳이 2way 아노바를 쓸 필요가 없다. 빼고 하면 된다. (변수는 적을 수록 좋으므로)

모델 비교

똑같이 이름이 anova인 함수인 함수를 사용, 같은 방식을 사용하나 봄

어쨋든 두 모델을 비교할 때 사용하는 함수이다. 특정 모델이 괜찮다고 말할 수 있는 근거가 된다.

( 성별은 의미가 없다고 하면 사람들이 의심한다 -> 두번째 모델이 좋다고 할 근거가 없습니다 )

> anova(modelA, modelC)

Analysis of Variance Table

Model 1: drugA_dose1 ~ fatigue
Model 2: drugA_dose1 ~ fatigue * patient.sex
  Res.Df    RSS Df Sum of Sq      F Pr(>F)
1     17 1.2285                           
2     14 1.1896  3   0.03883 0.1523 0.9265

GLM

통상적으로 반응변수가 Count Data이거나 Binary(True/False로 나뉘는 이항변수 같은 경우)인 경우에 사용